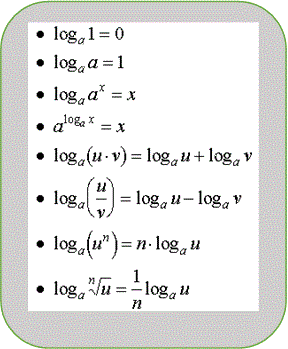CRITERIO DE LA PRIMERA DERIVADA APLICACIONES

PRIMERA DERIVADA:

Criterio de la primera derivada al método o teorema  utilizado frecuentemente en el cálculo matemático  para determinar los mínimos y máximos relativos  que pueden existir en una función  mediante el uso de la primera derivada, donde se observa el cambio de signo, en un intervalo abierto señalado que contiene al punto crítico c. 

Sea c un número crítico de una función f continua en un intervalo abierto I que contiene a c. Si f es derivable en ese intervalo, excepto quizás en c, entonces f''(c) puede clasificarse así:

1.     Si f '(x) cambia en c de negativa a positiva, f '(c) es un mínimo relativo de f.

2.    Si f '(x) cambia en c de positiva a negativa, f '(c) es un máximo relativo de f.

3.    Si f ' no cambia de signo en c (esto es f ' es positiva en ambos lados de c o negativa en ambos lados), entonces f carece de extremo local en c.

DERIVADAS

Derivada de una Función. La derivada de una función f, es una función denotada por f ′, tal que para cualquierx del dominio de f está dada por: 

si este límite existe.

 Si x1  es un número del dominio de f, entonces: 

si este límite existe.

 El proceso de calcular la derivada de una función se denomina derivación o diferenciación, es decir, la derivación o diferenciación es el proceso mediante el cual se obtiene f ′ a partir de f. Si una función tiene derivada en todo su dominio, se dice que es una función diferenciable.

Reglas básicas de derivación:

La regla de la constante:

La regla de la Potencia:

La regla de la suma y la diferencia:

La regla del Producto:

La regla del Cociente:

Derivadas de funciones trigonométricas:

Regla de la cadena:

CONTINUIDAD DE UNA FUNCION

Definición: Una función f(x) es continua en un punto x = así:

Dado  ∈ > 0, existe δ > 0 tal que siempre que |x − a| < δ, entonces |f(x) − f(a)| < ∈

Dicho de otra forma, si nos acercamos al punto a, entonces las imágenes se acercan a la imagen de a, f(a).

Si f(x) no es continua en x = a se dice que f(x) es discontinua en a o que tiene una discontinuidad en x = a.

Propiedad: Para que una función sea continúa en un punto a es necesario y suficiente que:

a) Exista el valor de la función en el punto, f(a).

b) Existan los límites laterales,

lim  f(x)

x→a+

y

lim f(x)

x→a−

, y sean finitos e iguales entre si e iguales a f(a), es decir:

lim  f(x)  =    lim    f(x) = f(a)

x→a+            x→a−

 

Esta ´ultima propiedad proporciona una forma muy sencilla de saber si una función es continua o no en un punto.

TIPOS DE DISCONTINUIDAD:

1.Existe f(a) y los limites laterales, que son iguales y finitos, pero distintos del valor de f(a). Una discontinuidad de este tipo se denomina discontinuidad evitable. 

    

Observamos que los limites por la derecha y por la izquierda valen 1, ambos, mientras que f(0) =0. Hay una discontinuidad evitable en x =0.

2. Existe f(a) y los limites laterales existen y son finitos, aunque distintos. Estamos ante una discontinuidad de salto finito.

En este caso el limite por la derecha es 1, el izquierdo es 0 y f(0) = −1/2 , hay una discontinuidad evitable en x =0.

3. Existe f(a) y alguno de los limites laterales es infinito. En este caso hay una discontinuidad de salto infinito.

Ahora f(0) =1, el limite por la izquierda vale 1 también y el limite lateral por la derecha vale+∞. Discontinuidad de salto infinito en x =0.

4. No existe f(a) o alguno de los límites laterales. Se trata de una discontinuidad esencial.

Los limites laterales, ambos, son +∞, pero f(0) no existe. Hay una discontinuidad esencial en x =0.

LIMITES DE UNA FUNCIÓN:

Se dice que una función f (x) tiene límite L en el punto x = a, si es posible aproximar f (x) a L tanto como se quiera cuando x se acerca indefinidamente a a, siendo distinto de a. En términos matemáticos, se expresa como: 

Se define el límite lateral por la derecha de a de la función f(x), y se expresa como:

lim     f(x)

x→a+

Al límite al que se acerca f(x) cuando x se acerca a  y toma valores mayores que a.

De igual modo, el límite lateral por la izquierda de a de la función f(x) se expresa como:

lim f(x)

x→a−

y se define como el limite al que se acerca f(x) cuando x se acerca a y toma valores menores que a.

TIPOS DE LIMITES:

1. Limites infinitos en un punto finito: En la situación del dibujo, se dice que el limite cuando x se acerca por la derecha de a es +∞, pues a medida que la x se acerca a, la función se hace cada vez mayor:

lim   f(x)=+∞

x→a+

(de igual forma se puede definir cuando nos acercamos por la izquierda. De igual modo se define el limite −∞ cuando nos acercamos a  (por la derecha o por la izquierda).

Puede ocurrir que uno de los limites laterales sea finito y otro infinito, o cualquier combinación entre ellos, por ejemplo:

lim f(x)=+∞

x→2+      

y

lim f(x)=2

x→2−     

2. Limites finitos en el infinito: Se dice que una función tiene límite b cuando x tiende a +∞

cuando la función se acerca a b cuando la x se hace cada vez mayor, es decir:

lim f(x) = b

x→∞

En este caso el límite es 2 cuando x tiende a +∞.

De igual modo se define el límite finito cuando x tiende a −∞. 

3. Limites infinitos en el infinito: Aparece este caso cuando si x tiende a +∞ la función se hace cada vez mayor o menor (lo mismo si x tiende a −∞).

Un ejemplo gráfico de este tipo de límites seria:

lim   f(x) = −∞

x→∞

• PROPIEDADES DE LOS LIMITES:

Dadas dos funciones f(x) y g(x) que tienen límite en un punto a, se cumplen las siguientes propiedades:

Estas propiedades se expresan matemáticamente como sigue:

APLICADA A LA ARQUITECTURA

La obra en Sungmam Korea se encuentra en un terreno de 330m2 que mantiene un contexto bastante exuberante en vegetación. Además de tomar en cuenta una cantidad de determinantes como : la inclinación del terreno y su forma irregular.

FUNCIONES

Una función es una relación establecida entre dos variables que asocia a cada valor de la

primera variable (variable independiente x), un único valor de la segunda variable (variable

dependiente y).

Esta relación se representa mediante y = f(x).

Las funciones se pueden determinar de varias formas:

• ·        Mediante una tabla de valores.
• ·        Mediante su expresión analítica.
• ·        Mediante su gráfica.

El DOMINIO de una función se puede obtener proyectando sobre el eje X cada uno de los puntos

de la gráfica.

El RECORRIDO de una función se puede obtener proyectando sobre el eje Y cada uno de los puntos

de la gráfica.

APLICADAS A LA ARQUITECTURA:

La sede del Banco Ciudad, creada por Norman Foster:

Tendrá 35.490 m2 repartidos en cinco pisos. 10.500 m2 de los cuales estarán reservados para unificar las áreas centrales del banco, hoy dispersas en 8 pisos.

FUNCIÓN EXPONENCIAL:

Una función exponencial con base b es una función de la forma f(x) = b^x , donde b  y  x son números reales tal que b > 0  y  b es diferente de uno.

El dominio  es el conjunto de todos los números reales y el recorrido es el conjunto de todos los números reales positivos.

• f(x) = 2^x                               

• Propiedades:

FUNCIÓN LOGARÍTMICA:

Una función logarítmica es aquella que genéricamente se expresa como f (x) == log_ax, siendo a la base de esta función, que ha de ser positiva y distinta de 1.

La función logarítmica es la inversa de la función exponencial , dado que:

log_a x = b Û a^b = x.

•  Propiedades:

                                              

APLICADAS A LA ARQUITECTURA:

Esta estructura de hierro pudelado diseñada por Gustave Eiffel aplica el algebra y el calculo infinitesimal para desarrollaar una ecuación adaptable al peso de la torre. Para ello emplearon una ecuación exponencial.

FUNCIONES TRIGONOMÉTRICAS:

Una función trigonométrica, también llamada circular, es aquella que se define por la aplicación de una razón trigonométrica a los distintos valores de la variable independiente, que ha de estar expresada en radianes. Existen seis clases de funciones trigonométricas: seno y su inversa, la cosecante; coseno y su inversa, la secante; y tangente y su inversa, la cotangente. Para cada una de ellas pueden también definirse funciones circulares inversas: arco seno, arco coseno, etcétera.

APLICADAS A LA ARQUITECTURA:

El teatro popular en Niteroi fue diseñado por el arquitecto Oscar Niemeyer en el año 2007.

Para el diseño de este edificio se utilizo una función trigonométrica que es la función seno.

Matrices en la Arquitectura

La matriz es una representación gráfica que permite descubrir cualquier tipo de relación deseada entre actividades, por medio de ejes cartesianos que se prolongan y forman una retícula, sobre la cual se vacían los datos deducidos.

Una retícula en 2 dimensiones compuesta por números o datos colocados en líneas o columnas. La cual es empleada para jerarquizar la importancia relativa de los locales, así como la relación entre ellos, indicándose el grado de atracción entre los mismos.

Las Matrices consisten en ver las zonas del programa arquitectónico y ver sus relaciones ya sea directo, indirecto y nulo.

Es un esquema organizado de intercomunicación entre los ambientes arquitectónicos planteado en función espacial, éstos son representados por figuras geométricas regulares de un mismo tipo (círculos, cuadros, etc) los cuales se ordenan de acuerdo a la relación que exista o debe existir entre ellos.

“SECCIONES CÓNICAS EN LA ARQUITECTURA”

LA PARÁBOLA:

En matemática , la parábola) es la sección cónica resultante de cortar un cono recto con un plano paralelo a su generatriz.

Se define también como el lugar geométrico de los puntos que equidistan de una recta (eje o directriz) y un punto fijo llamado foco.

En geometría proyectiva, la parábola se define como la curva envolvente de las rectas que unen pares de puntos homólogos en una proyectividad semejante o semejanza.

La parábola aparece en muchas ramas de las ciencias aplicadas, debido a que las gráficas de ecuaciones cuadráticas  son parábolas. Por ejemplo, la trayectoria ideal del movimiento de los cuerpos bajo la influencia de la gravedad.

APLICACIONES EN LA ARQUITECTURA

   Antigua Reserva Federal de Minneapolis

Un edificio destacable con una característica forma de PARÁBOLA es la antigua Reserva Federal de Minneapolis. El diseño es del Arquitecto de origen letón Gunnar Birkerts e imita un puente colgante.

Consiste básicamente en dos grandes estructuras laterales de hormigón separadas 100 metros una de la otra que sirven de soporte en las que se anclan dos inmensos cables de los que cuelga un edificio de 11 pisos.

Los cables adoptan una forma de curva catenaria que se reproduce en la fachada para resaltar el sistema constructivo empleado. 

Planta embotelladora de Mineapolis

Las tres bóvedas de la planta fueron construidas al mismo tiempo y para economizar costes Candela recurrió la forma de parábola hiperbólica pues permite la utilización de un encofrado recto.